الرنين المغناطيسي

الرنين المغناطيسي

(تجربة تأثير زيمان)

تأثير زيمان هو انفصال في خطوط الطيف المنبعثة من الذرة عندما تتعرض لمجال مغناطيسي خارجي. فمثلا لو كان لدينا ذرة ما لها انبعاث طيفي عند طول موجي 400nm فإنه عند تعرضها لمجال مغناطيسي خارجي سوف نلاحظ وجود انفصال في خطوط الطيف بمعني ظهور خط طيفي إضافي على جانبي الخط الأصلي له القيمة 399nm و 401nm. وحيث إن الخطوط الطيفية المنبعثة من الذرة تعكس لنا مستويات طاقة الذرة فانفصال الخطوط الطيفية يشير إلى انفصال في مستويات الطاقة بوجود المجال المغناطيسي.

كانت هذه إحدى نتائج النظرية الموجية لشرودنجر عندما طبقت على ذرة الهيدروجين والذرات الشبيه بالهيدروجين (أي تلك التي تحتوى على إلكترون واحد في مدارها الخارجي مثل ذرة الصوديوم). وقد قام العالم زيمان باكتشاف الانفصال في الخطوط الطيفية عند قام بتعريض الذرة لمجال مغناطيسي. وللتعرف على سيرة كفاح العالم زيمان العلمية اطلع على هذا الرابط http://nobelprize.org/nobel_prizes/p...eeman-bio.html

نظرية التجربة
[mark=CCCCCC] قبل البدء بشرح التجربة وفهم نتائجها سوف نقدم مختصر عن نظرية التجربة والتي تتعلق بفهمنا لنموذج بور للذرة وكذلك نتائج النظرية الموجية، فكما نعلم إن هناك مدرستين في الفيزياء المدرسة الكلاسيكية والمدرسة الكوانتمية، ولقد انتقلت العلوم الفيزيائية نقلة نوعية بعد النظرية الكمية وأصبحت الأمور الغامضة والمبهمة لها تفسير. فالنظرة الفيزيائية للظواهر التي تكون على المستوى الذري لا يمكن تفسيرها إلا من خلال المدرسة الكوانتمية. لأننا نتعامل مع أبعاد متناهية في الصغر تفوق في صغرها الطول الموجي للضوء الذي نستخدمه لنرى به الكون من حولنا، وهنا لا نستطيع أن نستخدم الميكانيكا الكلاسيكية في فهم ما يحدث على البعد الذري ولذا تظهر حاجتنا الماسة لميكانيكا الكم والنظرية الموجية.[/mark]

النظرة الكلاسيكية للذرة تشبه حركة الإلكترون حول النواة بحركة الأرض حول الشمس أو حركة القمر حول الأرض، ولذلك سميت هذه النماذج الافتراضية للذرة بالنموذج الكوكبي planetary model وكانت قيم الطاقة وعزم كمية الحركة المدارية للإلكترون هي قيم مستمرة أي يمكن أن تأخذ كل القيم الممكنة بدون قيود تذكر، وكذلك اتجاه العزم في الفراغ غير مقيد أيضا ويمكن أن يكون في أي اتجاه. إن هذا التشبيه لا يتفق مع تنبؤات الميكانيكا الموجية التي اخذت في الحسبان الخاصية المزدوجة للإلكترون. فمستويات الطاقة محددة ولها قيم معينة حددتها بالعدد الكمي الرئيسي n وكذلك عزم كمية الحركة المدارية محدد بقيم معينة ولها عدد كمي يرمز له بالرمز l والذي يسمى العدد الكمي المداري، هذا بالإضافة إلى ان مركبة عزم كمية الحركة المدارية بالنسبة لمحور ثابت في الفراغ بالعدد الكمي ml والذي يسمى بالعدد الكمي المغناطيسي.

ولأوضح لكم أعزائي الفرق بين النظرة الكلاسيكية والنظرة الكوانتمية دعونا نستخدم الجايروسكوب وهو كما في الشكل أدناه عبارة عن حلقة أو عجل متوازن ومثبت على عمود في الوسط تماما يمر بمركز الحلقة ونسميه المحور. وعندما بجعل الحلقة تدور بسرعة عن طريق لف محورها بقوة، فإننا نشبه ذلك بدوران الإلكترون حول النواة حيث تمثل الحلقة مسار الإلكترون حول النواة. والمحور يمثل اتجاه كمية الحركة الزاوية للإلكترون حول النواة L.

دوران محور الجايروسكوب يكون رأسيا إذا كان مستوى دوران الحلقة موازياً لسطح الأرض اما اذا كان محور الجايروسكوب يصنع زاوية مع العمودي على سطح الأرض فان محور الجايروسكوب سوف يدور حول العمودي على الأرض في مسار على شكل مخروط وهذه الحركة نسميها Larmor precession.

المقصود بهذا المثال هو تشبيه لما يحدث في الذرة حيث إن الإلكترون يدور حول النواة وهو مسار حلقة الجايروسكوب وللإلكترون كمية حركة مدارية عمودية على مستوى الدوران وهذا نمثله بمحور الجايروسكوب ولكن مع فارق الأبعاد.

في المدرسة الكلاسيكية يسمح لمحور الدوران أن يتخذ أي زاوية بالنسبة للعمودي على الأرض للدوران حولها ولكن في المدرسة الكوانتمية يسمح لكمية الحركة المدارية للإلكترون أن تتخذ زوايا ذات قيم محددة فقط أي أن اتجاه كمية الحركة المدارية L مكمم في الفراغ.

[mark=99CCFF]ملاحظة: من خلال معرفتنا لاتجاه كمية الحركة المدارية L للإلكترون حول النواة نستطيع أن نعرف مداره حول النواة وشكله لان المتجه L دائما يكون عموديا على مستوى مدار الإلكترون واتجاهه يحدد من خلال قبضة اليد اليمنى بحيث إن أصبع الإبهام في اتجاه المتجه L وباقي الأصابع تشير إلى دوران الإلكترون حول النواة.[/mark]

تعطى كمية الحركة المدارية للجايروسكوب بالعلاقة
[align=center]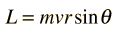[/align]

ولكن العالم بور الذي ادخل الميكانيكا الكوانتمية في فرضياته افترض إن كمية الحركة المدارية تأخذ القيمة

[align=center]L = n h/2pi [/align]

وقد توصل بور لهذه العلاقة من خلال تطبيق فرضية دبرولي على كمية الحركة المدارية L بان عوض عن السرعة v بما تنبأت به فرضية دبرولي ولمعرفة التفاصيل استعن بهذا الرابط في الجزء الثاني المعنون بـ Angular Momentum Quantization

أي أن

[align=center]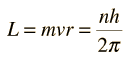[/align]

وكان هذه الفرضية هي سر نجاح نموذج بور ذرة الهيدروجين وقد أكدت النظرية الموجية (ميكانيكا الكم) إن فرضية بور صحيحة وان كمية الحركة المدارية مكممة ولكن مع اختلاف المعادلة حيث أعطت النتيجة التالية:

حيث l هو العدد الكمي المداري.

كما إن النظرية الموجية أيضا تنبأت بوجود عدد كمي أخر هو العدد الكمي المغناطيسي ml والذي يحدد مركبة المتجه L بالنسبة للمحور الافتراضي (العمودي على الأرض بالنسبة لمثال الجايروسكوب) وسميت بالمركبة Lz

[align=center]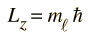[/align]

والذي يأخذ قيم محددة تعتمد على العدد الكمي l بمعنى لو كانت l=1 فان ml تأخذ القيم -1 , 0 , +1 وإذا كانت l=2 فان ml تأخذ القيم -2, -1, 0, +1, +2 وهكذا بمعنى القيم تكون عبارة عن 2l+1 قيمة. وهذا ما كان لابد من تجربة لتؤكده، وكانت هذه التجربة هي تجربة زيمان.

لتوضيح ذلك بالرسم سوف نستعين بمتجه العزم المداري L والذي يكون عمودياً على مستوى مدار الإلكترون حول النواة وهو ممثل في الشكل التالي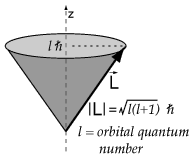

الزاوية التي يتخذها متجه العزم المداري مكممة وتحدد بالعدد الكمي المغناطيسي والشكل التالي يوضح المواقع التي سوف يتخذها في الفراغ حول محور z

[align=center]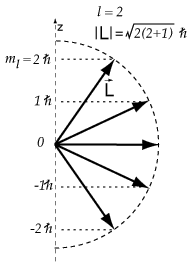[/align]

وهذا يحدد مستوى المدار الذي يتخذه الإلكترون حول النواة وكما تلاحظ فهو مكمم.

[mark=CCCCCC]تجربة زيمان أجريت للتأكد من صحة هذه النتائج من خلال تعريض الذرة لمجال مغناطيسي خارجي ولكن قد تتساءل عزيزي القارئ ما علاقة المجال المغناطيسي الخارجي هنا في الموضوع؟ وهل تتأثر كمية الحركة المدارية بالمجال المغناطيسي؟، أقول لك معك حق في هذا ولكن إذا علمنا إن كمية الحركة المدارية للإلكترون مرتبطة مع العزم المغناطيسي للإلكترون. العزم المغناطيسي ناتج من حركة شحنة في مدار دائري (مثل حركة الالكترونات في السلك ينشىء عنه مجال مغناطيسي) إذا هناك عزم مغناطيسي للإلكترون حول النواة وهو مرتبط مع كمية الحركة المدارية من خلال العلاقة[/mark]

[align=center]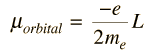[/align]

ويكون العزم المغناطيسي في اتجاه معاكس لمتجه كمية الحركة المدارية. وعلى هذا الأساس يكون متجه العزم المغناطيسي أيضا مكمم، وبالتالي فإن تأثر كمية الحركة المدارية بالمجال المغناطيسي الخارجي هو تأثر بطريقة غير مباشرة أي من خلال العزم المغناطيسي إذا تغير اتجاهه فان متجه كمية الحركة المدارية سوف يتغير.

يؤثر المجال المغناطيسي الخارجي على العزم المغناطيسي للإلكترون بعزم ازدواج وتكون الطاقة التي اكتسبها الإلكترون من المجال المغناطيسي ليغير اتجاهه هي على النحو التالي

[align=center]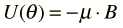[/align]

وبالاستفادة من العلاقة التي تربط كمية الحركة المدارية مع العزم المغناطيسي

[align=center]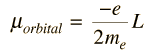[/align]

نحصل على

[align=center]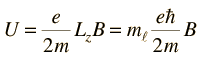[/align]

وهذا يوضح إن هناك زيادة في الطاقة لكل مستوى محدد بالعدد الكمي ml وان هذه الزيادة تتناسب طرديا مع شدة المجال المغناطيسي. ولحساب مقدار الزيادة في الطاقة نعوض عن الثوابت في المعادلة أعلاه لنحصل على

[align=center]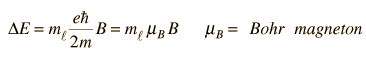

[img]http://hyperphysics.phy-astr.gsu.edu/hbase/quantum/imgqua/mub.gif[/img[/align]]

وهكذا نستنتج إنه عندما تتعرض الذرة لمجال مغناطيسي فان مستويات الطاقة تنفصل عن بعضها البعض بمقدار ثابت يعتمد على العدد الكمي ml والمجال المغناطيسي، وعليه يكون الطيف المنبعث من الذرة منفصل أيضا بنفس المقدار، وهذا ما قام باثباته عمليا العالم زيمان حيث وجد انفصال في خطوط الطيف عندما تتعرض الذرة لمجال مغناطيسي، وكانت لهذه التجربة صدى كبير في التحقق من نتائج النظرية الموجية للوصف الذرة.

الشكل أدناه (الجزء الأيسر) يعبر عن حالة مستويين للطاقة بدون وجود مجال مغناطيسي و(الجزء الأيمن) يوضح انفصال هذين المستويين في وجود مجال مغناطيسي خارجي. حيث ينفصل المستوى l=1 إلى ثلاثة مستويات بينما ينفصل المستوى l=2 إلى خمس مستويات كما وضحنا مسبقا بناءً على العلاقة بين ml و l وان لكل l يوجد عدد 2l+1 من الحالات ml.

[align=center][/align]

[mark=CCCCCC]عند انتقال الالكترونات المثارة إلى مستويات الطاقة الأقل أي من المستوى l=2 إلى المستوى l=1 بدون وجود المجال المغناطيسي ينبعث عن كل انتقال فوتون يحمل فرق الطاقة بين المستويين ونرصد هذا الفوتون بواسطة المطياف على شكل خط طيفي حاد. ولكن عندما تتعرض الذرة إلى مجال مغناطيسي خارجي تنفصل مستويات الطاقة وينتج عن ذلك خمس مستويات للمستوى l=2 وثلاث مستويات للمستوى l=1 وبالتالي يكون هناك أكثر من خيار لانتقال الالكترونات من المستويات المثارة إلى المستويات الأقل طاقة والقاعدة التي تحكم انتقال الالكترونات بين مستويات الطاقة هي [/mark]

[align=center]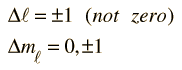[/align]

[mark=CCCCCC]ولهذا يكون هناك ثلاثة مجموعات من الانتقالات هي التي يكون فيها الفرق في العدد الكمي المغناطيسي يساوي صفر وهي المجموعة الأصلية ومجموعة ثانية يكون فيها الفرق يساوي -1 ومجموعة ثالثة يكون فيها الفرق يساوي +1 وهذه المجموعات الثلاثة تظهر على شكل ثلاثة خطوط طيفية منفصلة.[/mark]

إذا نستنتج من ذلك إن الخط الطيفي المنبعث من إثارة ذرة ينفصل في حالة تعرض الذرة إلى مجال مغناطيسي خارجي وهذا يشير إلى انفصال في مستويات الطاقة. وبحساب مقدار التغير في التردد نستطيع أن نحسب مقدار الانفصال في مستويات الطاقة بدقة. وبالتالي نتحقق من نتائج النظرية الموجية وهذا ما قام به العالم زيمان.

تجربة زيمان
تعتمد تجربة زيمان على توفير مصدر لمجال مغناطيسي قوي بحيث يصل إلى 1 تسلا على الأقل أي 10,000 جاوس وذلك لنتمكن من فصل مستويات الطاقة إلى مدى نستطيع رصد الطيف الناتج عنه بواسطة المطياف كما في الشكل

يتم وضع مصباح صوديوم أو سيزيوم أو زئبق بين قطبي المغناطيس وسنفترض اننا نستخدم مصباح به غاز الصوديوم. وبدراسة الطيف المنبعث منه بدون وجود المجال المغناطيسي، ثم دراسة الطيف المنبعث بوجود المجال المغناطيسي وقياس الانفصال في الخطوط الطيفية التي تظهر على جانبي كل خط أصلي. ومقارنة مقدار الانفصال في التردد بالانفصال في مستويات الطاقة المتوقع حسب المعادلة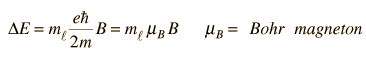

نكون قد تحققنا من الانفصال في مستويات الطاقة حسب العدد الكمي المغناطيسي ونكون أيضا قد أثبتنا أن كمية الحركة المدارية للإلكترون مكممة.